Chair Angle Calculator
Background
The legs of a chair are often angled from the vertical. The side-to-side and front-to-back components of these angles are called splay and rake, and are easy to measure off a photograph of a chair. But when making a chair, it is easier to resolve the splay and rake into a single resultant angle along the sightline. Christopher Schwarz talks about this in The Stick Chair Book (PDF excerpt):
If you know the rake and splay that you want for your legs, you can use trigonometry to convert that to sightlines and resultants. There are equations, tables and calculators out there to guide you on that math path. (155)
Schwartz cites Drew Langsner's The Chairmaker's Workshop as giving the best description of sightlines and resultants. This book provides an overview of the method, the diagram below showing how these angles are laid out on a chair seat (from page 291), and tables of the computed sightline and resultant given the rake and splay which is helpful for checking my calculations below.
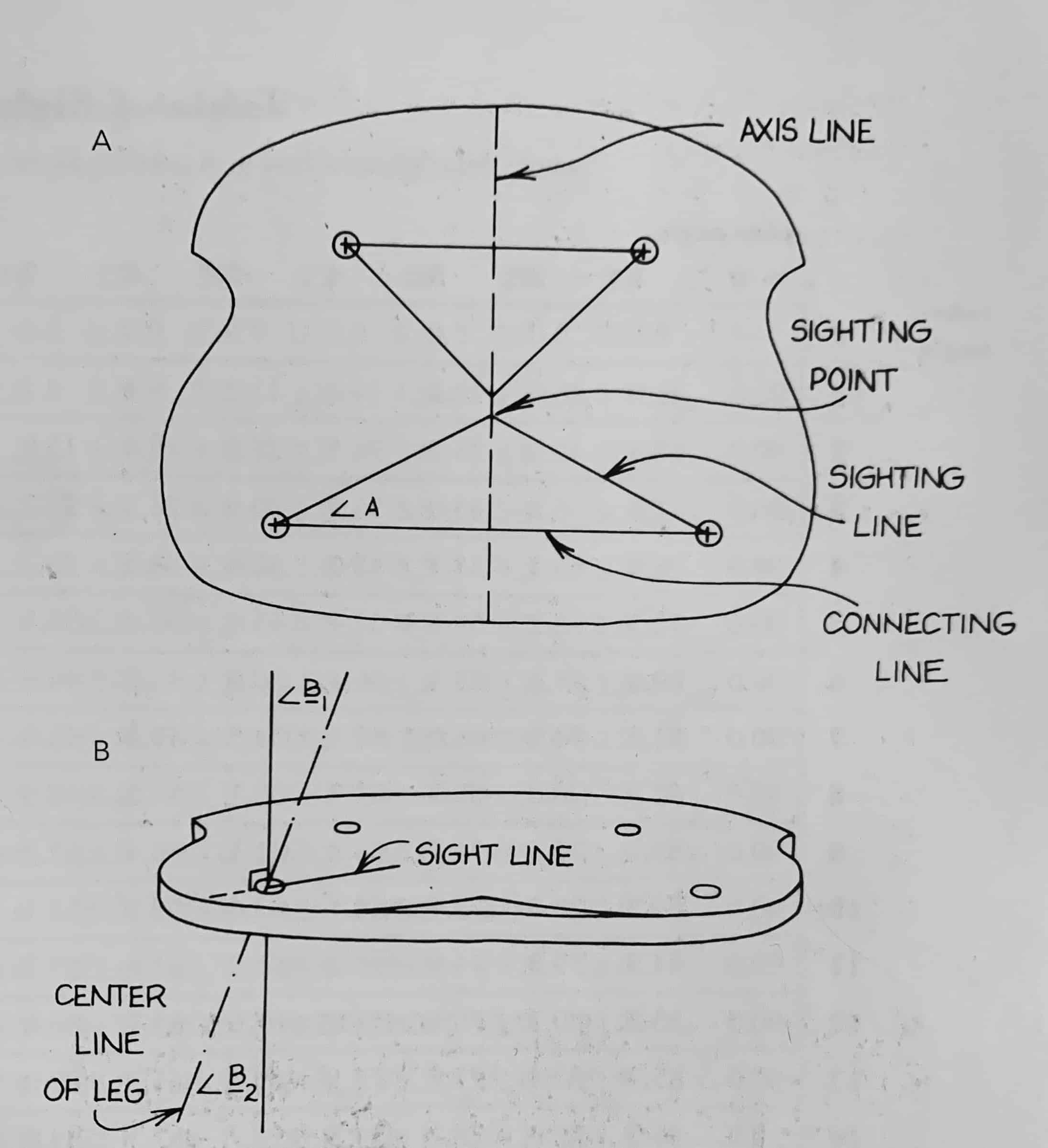
A derivation is not provided in either of these sources, so I provide one here. Thanks to Woodworking in a Tiny Shop for providing his solution which helped me catch an error in my first version.
Derivation
In the diagram below, we are given the angles of splay (s) and rake (r), and we will compute the sightline angle ($\alpha$) and the resultant angle ($\theta$).
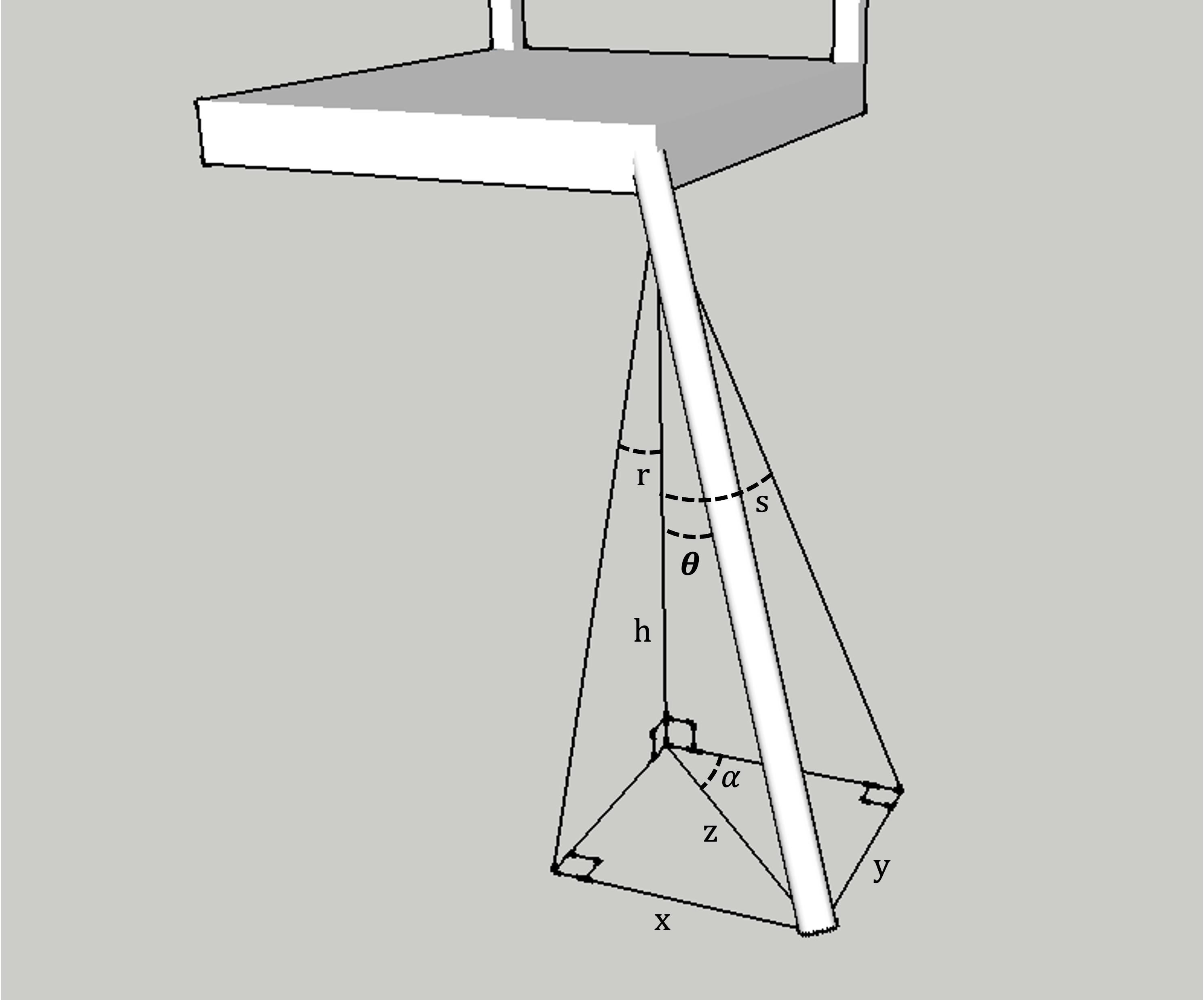
Recall the trigonometric relationships of SOH, CAH, TOA.
First we need expressions for $x$ and $y$:
$$\tan(s) = \frac{x}{h} \rightarrow \boxed{x=h\tan(s)}$$
$$\tan(r) = \frac{y}{h} \rightarrow \boxed{y=h\tan(r)}$$
Then we write an expression for the sightline angle $\alpha$:
$$\tan(\alpha)=\frac{y}{x}=\frac{h\tan(r)}{h\tan(s)}$$
$$\text{sightline: } \boxed{\alpha=\tan^{-1}\left(\frac{\tan(r)}{\tan(s)} \right)}$$
Next to compute the resultant angle $\theta$, we need an expression for $z$:
$$x^2+y^2=z^2$$
$$z=\sqrt{x^2+y^2}$$
Substituting for $x$ and $y$ from above:
$$z=\sqrt{h^2\tan^2(r)+h^2\tan^2(s)}=h\sqrt{\tan^2(r)+\tan^2(s)}$$
Now we can write an expression for $\theta$ and substitute in the above:
$$\tan(\theta)=\frac{z}{h}$$
$$\tan(\theta)=\frac{h\sqrt{\tan^2(r)+\tan^2(s)}}{h}$$
$$\tan(\theta)=\sqrt{\tan^2(r)+\tan^2(s)}$$
$$\text{resultant: } \boxed{\theta=\tan^{-1}\left( \sqrt{\tan^2(r)+\tan^2(s)} \right)}$$
This is implemented in the following sheet: Chair Angle Calculator - Google Sheets
Resources
- Coming Soon: The Chairpanzee – Lost Art Press
- New Video: How to Use the Chairpanzee – Lost Art Press
- New in the Store: The Chairpanzee – Lost Art Press
- Woodworking in a Tiny Shop: Resultant and Sightline Angle Calculator
Created: 2022-07-05-Tue
Updated: 2023-06-01-Thu